VECTORES

VECTORES 

El concepto de vector presenta múltiples acepciones, en matemáticas lo entendemos como una magnitud física de longitud (módulo) y orientación (dirección) determinada que está representada geométrica-mente como segmentos de recta.

• ¿QUE SON VECTORES?

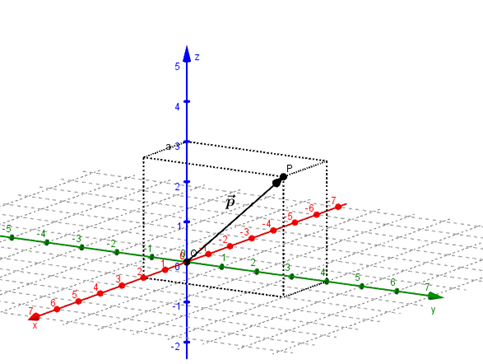
Un vector es una expresión geométrica que se extiende desde un punto de referencia llamado origen, hacia otro punto que se denomina extremo. El concepto de vector hace referencia a la idea de desplazamiento en el espacio desde un espacio inicial a un espacio final.

• OPERACIONES CON VECTORES

SUMA DE VECTORES:

Si se suman dos magnitudes escalares, basta con sumar sus valores numéricos. Por ejemplo 10 w más 20 w son 30 w de potencia. Por el contrario, para la suma de vectores el proceso es más complejo, pues debemos de tener en cuenta dirección y sentido.

Conociendo las componentes cartesianas de los vectores a sumar, el vector resultante tendrá como componentes cartesianos la suma, eje a eje, de cada vector.

Si queremos sumar dos vectores en 3D y conocemos sus componentes, las componentes del vector suma, aplicando el mismo procedimiento, sería:

• EJEMPLO:

Vamos a sumar dos vectores en tres dimensiones de los que sabemos sus coordenadas cartesianas:

• RESTA DE VECTORES: 

Para la resta de vectores, se procede igual que en la suma de vectores, bien operando con los componentes cartesianos, o bien mediante el método del paralelogramo.

Sabiendo los componentes cartesianos de los vectores, restaremos las componentes cartesianas del segundo vector de los del primero:

EJEMPLO:

Sean los vectores =(2,-3,4) y el vector =(3,4,-2), obtener la resta de vectores –:

(-1, -7, 6) serían las coordenadas x, y, z del extremo del vector resta.

El mismo procedimiento serviría para restar dos vectores en el plano, de ejes x e y.